Величайшая история о разработке приложений-калькуляторов: как Google создал почти идеальный инструмент

^{Оригинал на тошноте}

Калькулятор должен показать вам результат вашего математического выражения, что намного, намного сложнее, чем кажется. Я расскажу вам самую большую историю разработки кластера приложений. Взгляните на калькулятор в iOS. Вы что -то замечаете? Это показывает не тот результат. (10^100) + 1 — (10^100) — это 1, а не 0. В Android результат веренС И история о том, как такая вещь произошла, абсолютно сумасшедшая.

Google нанимает Hans-y. Боэм, который хорошо известен. Им нужен был элитный программист, чтобы устранить ошибки памяти и параллельного программирования. Он направляет усилия по определению семантики общих переменных C ++. Но затем они дают ему один, так как это оказывается невозможной задачей: написать кластер приложений.

Даже для него это было проблемой. Цель кластера приложений-дать вам правильные ответы. Плавающие номера запятых неточны — они не могут выразить значения, такие как 0,3 или 10^100. Это означает, что калькулятор, основанный на плавающих числах запятой, похож на дом, построенный на песке.

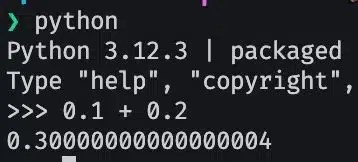
Стоит повторить: чтобы дать правильные ответы на математические выражения, калькулятор должен представлять цифры. И на практике не все цифры могут быть представлены в IEEE с плавающей запятой. Даже простые операции с плавающими номерами запятой требуют тщательного рассмотрения, чтобы получить правильный ответ.

Например, алгоритм суммирования Кахана (Алгоритм суммирования кахана) значительно уменьшает численную ошибку при сборе последовательности плавающих чисел запятых с крайней точностью по сравнению с обычным (наивным) подходом. Алгоритм работает, поддерживая отдельную «текущую компенсацию» — переменную, которая накапливает небольшие ошибки. Это решение фактически приводит к повышению точности точности переменной компенсации.

Первое решение: большие числа

Некоторые проблемы можно избежать, используя большие числа. Большинство численных типов используют 2 или 4 байта. Но не большие цифры. Это целые числа без ограничений. Они занимают столько памяти, сколько им нужно. Это решает проблему с примером (10^100) + 1 — (10^100). Но большое количество — это целые числа. А как насчет дробных чисел?

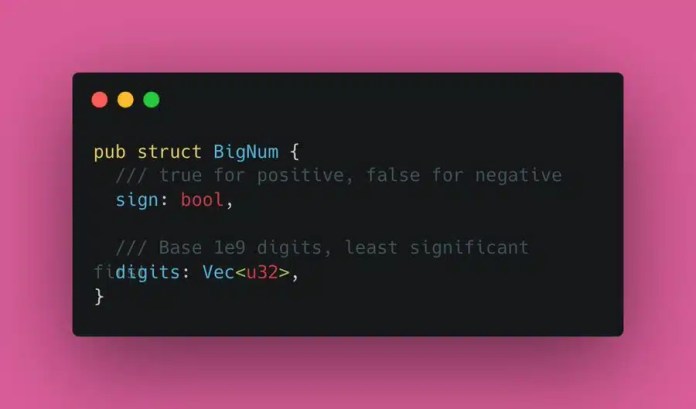
Loca может быть легко рассчитана. Большие числа должны быть просто использованы для числителя и знаменателя. Выполнение арифметических операций для этого типа данных тривиально и всегда дает точные ответы. Многие объявили бы победу по этому поводу. Но Боэм не был доволен. Он даже не был доволен.

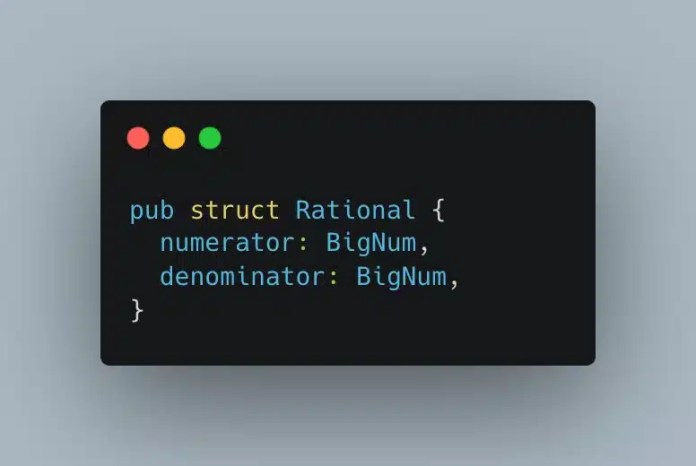
Математика — это гораздо больше, чем дробные числа. Как насчет π или √2? Калькулятор на основе урожая не сможет рассчитать окружность круга, поскольку π не может быть выражен в виде печени. Если ваш калькулятор не может справиться с математикой 9 -го класса, что вам нужно?

Алгебраическая арифметика

Алгебраическая арифметика приблизит его к конечной цели. Забудьте о представлении чисел в качестве цифр и знаменателей. Вы можете представить их как полиномиальное уравнение, на которое они отвечают. Для √2 это будет x² — 2 = 0. (Более того, это будет помнить, что ему нужен положительный корень.)

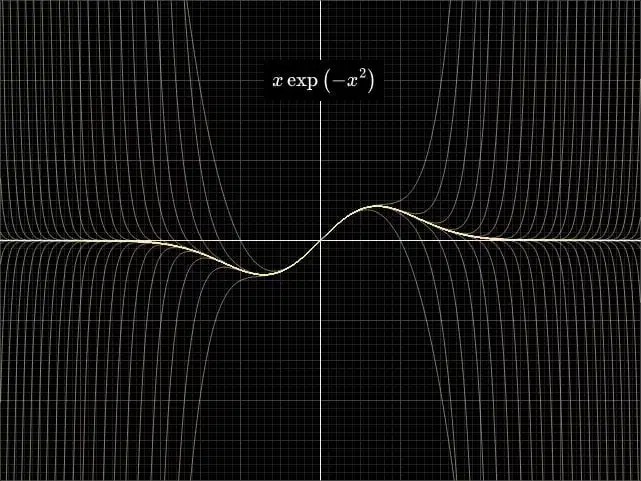
В этой ситуации математические операции становятся немного более сложными для выполнения:

Новый мульти -член (полиномиальный), корень которого является суммой исходных многочисленных измерений, должна быть создана для сбора
Для умножения используется композиция мульти -члена и полученного многолетнего члена.

Вы можете догадаться, что этого недостаточно для Бо. Это работает только для алгебраических чисел. Но это не дает π.

Конструктивные реальные числа

Так что Боэму нечего делать, кроме углубления в теме. Пришло время серьезно относиться к этому калькулятору. Это началось с целых чисел (Bignum), перенесено на рациональные числа, а затем в алгебраические числа. Что дальше? Конструктивные реальные числа (строго говоря, Мы смотрим на конструктивные способы составления реальных чисел)

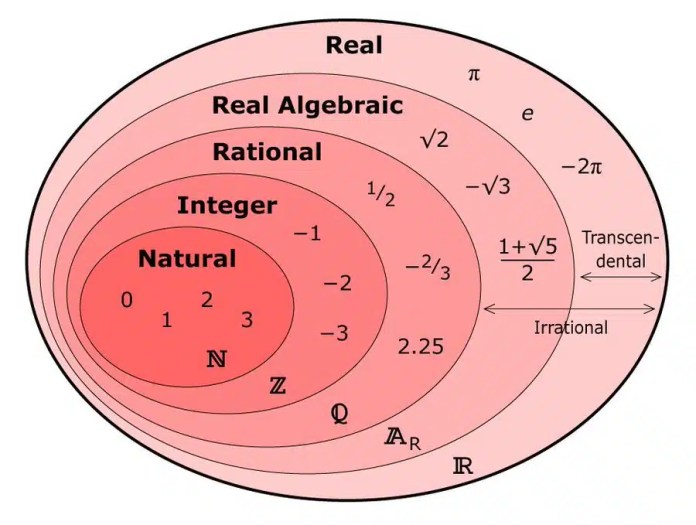
В результате Boem начал изучать «затворническую настоящую арифметику» (RRA). Если у вас есть выражение, и вы знаете, какая точность должен быть ответ, RRA даст вам ответ с точностью, не ниже, чем тот, который набор.

Конструктивные реальные числа числа, которые вы можете рассчитать более точно и точнее. Вы никогда не сможете указать мне все десятичные фрагменты числа π. Но если я попрошу вас назвать рациональный номер с точностью до 0,01 числа π, вы сможете назвать меня 3.14. Число π находится в пределах 0,01 от числа 3.14, так что это правильный ответ.

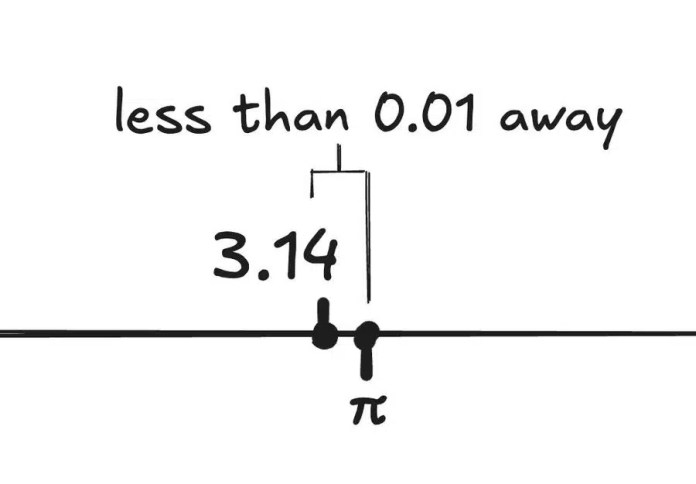
Теперь давайте предположим, что я прошу вас рассчитать число с точностью до 0,01 из 2π. Вы знаете, как рассчитать количество числа π. (314159…) Затем вы можете забрать некоторые из них и умножить их на 2.

Если вы умножите номер на 2, ошибка удваивается. Я попросил вас рассчитать 2π до точности до 0,01, поэтому вам необходимо вычислить π до точного до 0,005. Допустим, вы получите 3141, что на самом деле меньше 0,005 от π. Умножьте этот номер на 2, и все готово!

Как работает RRA (рекурсивная лучшая акустика)

Любое число в RRA представлено как функция, которая принимает рациональный номер и возвращает рациональное число. Рациональный номер, который он принимает, является необходимой ошибкой. Гарантируется, что рациональный номер, который он возвращает, находится в рамках этой ошибки реального числа, который он фактически представляет.

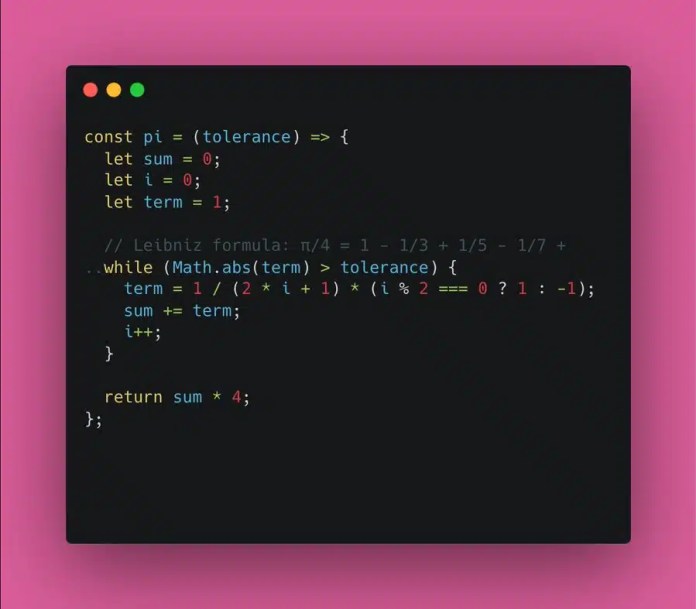
Это означает, что RRA легко использовать. Вы указываете, насколько точно вы хотите, чтобы ответ был, и он рекурсивно определяет, какая точность необходима для всех промежуточных расчетов. Он не обрабатывает проблем с выражениями, содержащими π или √2. Это очень важно для калькулятора.

Новые проблемы

Вы думаете: «Конечно, Бом остановится здесь». Вам просто нужно установить «Точность вывода» на количество номеров, отображаемых калькулятором, верно? Тогда все числа, показанные калькулятором, будут правдой. Таким образом, калькулятор всегда будет выявлять правильный ответ сейчас!

Но это не будет. Когда пользователи вводят «1-1», ответ равен 0, поэтому он должен отображаться «0». Но RRA только скажет вам, что «1-1 находится в пределах ошибки от 0,0000000000000». Показывая 0,0000000000000 на экране, когда ответ ровно 0, будет ужасной проблемой пользователя.

Boem возвращается на чертежную доску. В этот момент он, должно быть, был довольно обеспокоен. По сравнению с этим, «эффективно с точки зрения пространства, консервативная очистка памяти» была детской игрой. Он не мог справиться с этим в одиночку. Он обратился за помощью к выдающимся коллегам, таким как Корки Картр и Вернон Ли -младший.

Вы можете проверить, что два числа RRA не равны. Вы можете рассчитать их с повышением точности, когда видите, где они отличаются. Но если цифры равны, вы рассчитываете их с повышением точности до конца. Это не приведет к завершению процесса.

Помните: если калькулятор показывает 0 для E^(-10000), то это было бы неверно. Это не 0. Это должно быть 0,00000… .. и вы можете прокрутить, пока не увидите первую цифру. Но когда вы входите в SIN (π), это должно быть 0. SIN (π) равен 0. RRA не может показать нам это!

Или вы просто не можете дать ответ, как калькулятор делает в iOS.

Следовательно, точный ответ не может быть получен с помощью структурных реальных чисел. Но Боэм и его коллеги понимают, что это вполне возможно. Нет необходимости работать со всеми конструктивными реальными числами. Необходимо работать только с теми цифрами, которые могут быть выражены с помощью операций, доступных в калькуляторе.

Прорыв

Задача состояла в том, чтобы определить Равны ли два структурных реальных числаС Было невозможно решить. Они упростили задачу и подошли к решению, ограничивая способы, с помощью которых цифры могут быть составлены:

Четыре основных арифметических операций и квадратных корней
Тригонометрические функции SIN, COS и TAN и их обратные значения
Экспоненциальные и (естественные) логарифмические функции

Это гораздо меньший набор чисел, чем все конструктивные реальные числа. На самом деле, кто -то уже исследовал эту проблему. Это Дэн Ричардсон и Джон Фитч, которые решили задачу в 1994 году.

Их решение абсолютно правильное. Авторы разработали полуалгоритм, который сначала уменьшает задачу для проверки эквивалентности элементарных констант, а затем решает ее. Характерной особенностью этого алгоритма является то, что он всегда дает правильный ответ, когда он будет завершен и гарантированно закончится, если только задача не содержит счетчика для гипотезы Шнуэля.

Это звучит идеально. Но есть одна проблема. Алгоритм слишком медленныйС 1 не равен 1-e^(e^(e^(-1000))). Но для алгоритма Ричардсона и Фиха, чтобы найти это, потребуется больше шагов, чем атомы во вселенной. Калькулятор Android должен работать. По словам мягко, быстрее.

Они понимают, что это не конец света, если они показывают «0,000000 …», когда ответ ровно 0, хотя это не идеальный пользовательский опыт. Они просто не могут показать «0» на случай, если ответ 0,0000001.

RRA дает вам полную силу структурных реальных чисел, но недостаток заключается в том, что получение точных ответов становится невозможным. Рациональная арифметика дает вам точные ответы, но она не может выразить π. Можно ли объединить их сильные стороны?

Хотя статья заканчивается немного неожиданно, комментарии под ней очень много, с огромным количеством примеров и скриншотов того, каким результатом является введение задачи расчета (10^100) + 1 — (10^100 )

Например, один пользователь говорит, что калькулятор Hyper Calc Pro дает 0. Другие акции, которые SpeedCrunch дает 0, за исключением того, что калькулятор в Windows 10 и Windows 11 неожиданно дает правильный ответ — 1.

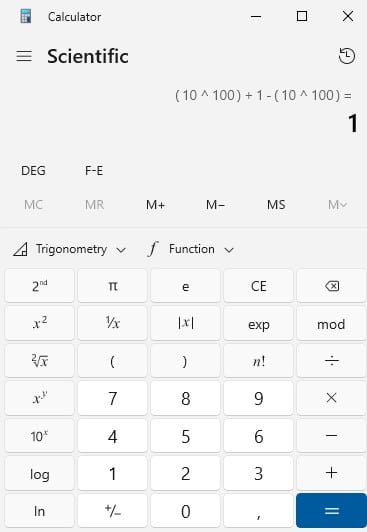
Конечно, любой может проверить самостоятельно, но есть примеры, которые iPhone 15 дает 0, но Android 15 дает 1. С другой стороны, калькулятор Android 9 дает неправильный 0. Странно…